Rate Limiters

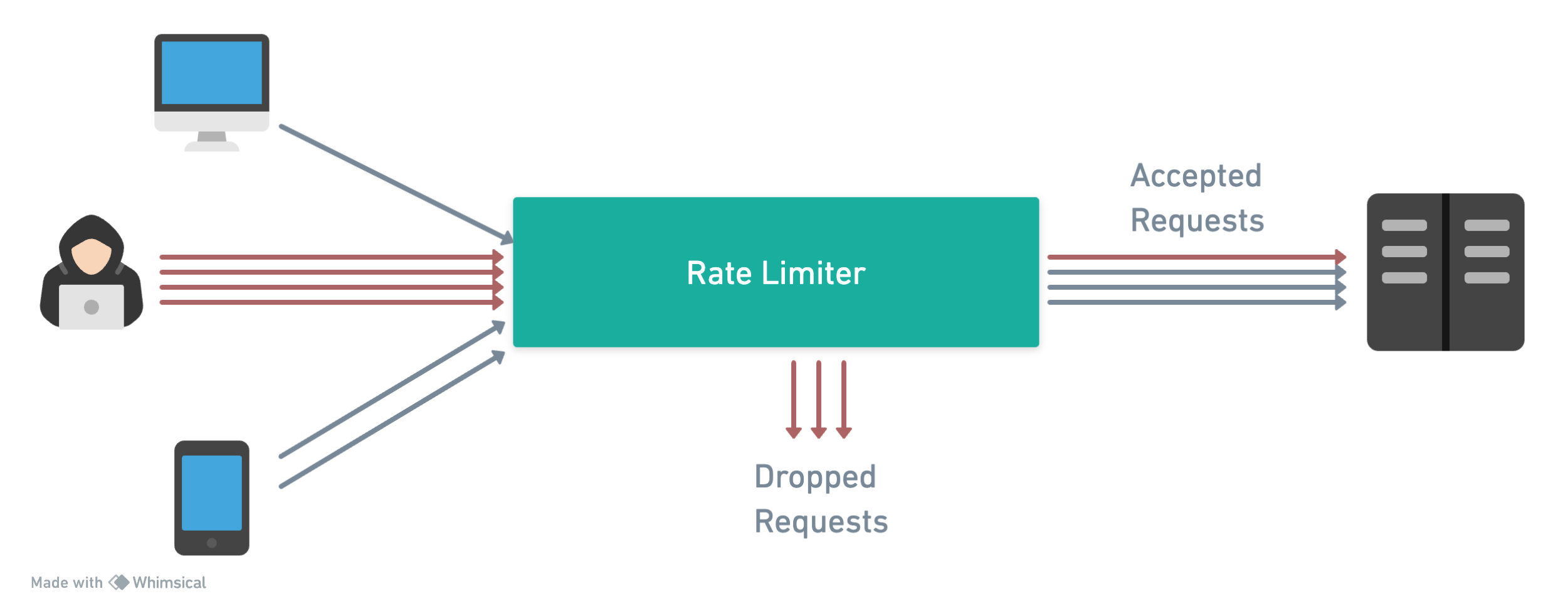
In this blog post, we'll discuss rate limiters, a critical component in distributed systems to prevent abuse and ensure fair usage of resources. We'll cover the different types of rate limiters and their implementations in the minimalist-java framework, and we'll provide examples of how to use them with the minimalist-java http-api module.

---

Token Bucket

The token bucket algorithm is a simple and efficient way to control the rate of requests to a resource. It is widely used in network traffic shaping, API rate limiting, and other scenarios where a controlled flow of requests is required.

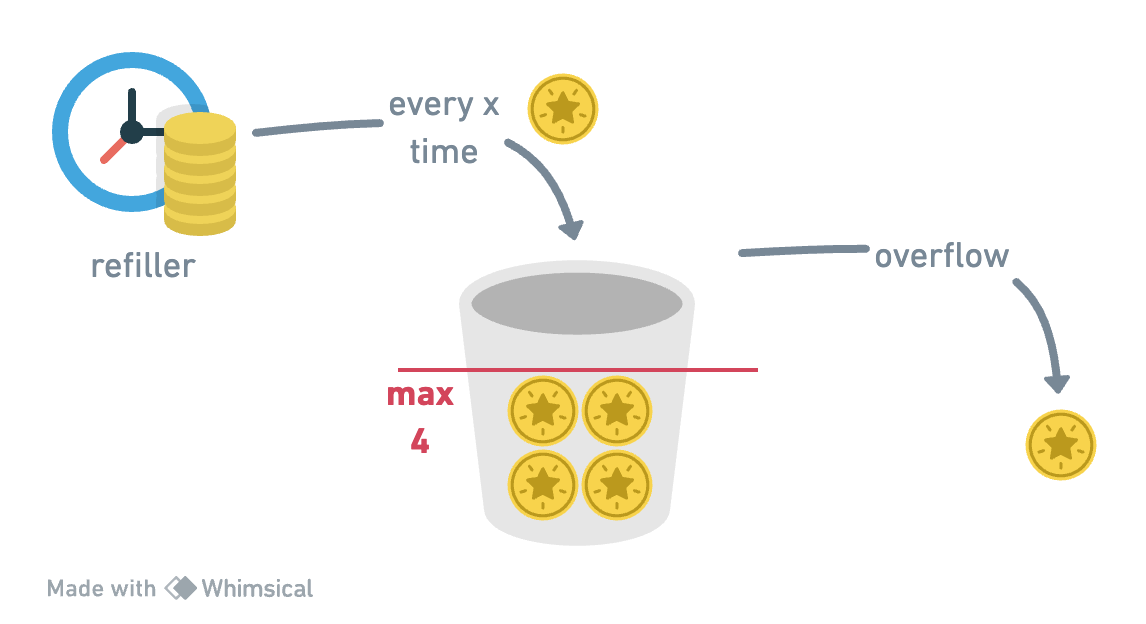
The token bucket algorithm is based on the concept of a bucket that holds a fixed number of tokens.

• When a request arrives, the algorithm checks if there are enough tokens in the bucket to serve the request.
• If there are enough tokens, the request is served, and the number of tokens in the bucket is decremented.
• If there are not enough tokens, the request is rejected.
• Periodically, the bucket is refilled with a fixed number of tokens.
• The bucket has a maximum capacity, and the number of tokens is never greater than the capacity.
• The rate at which the bucket is refilled determines the maximum rate at which requests can be served.

Example: bucketSize = 5, refillRate = 1 token/sec.

• T0 (01:00:00.000): Bucket starts full with 4 tokens.
• T1 (01:00:01.100): 1 request arrives, consumes 1 token, 3 tokens left.
• T2 (01:00:01.200): 3 more requests arrive, consume 3 tokens, bucket empty.
• T3 (01:00:01.300): No tokens, requests dropped. Bucket refills 4 token per second.
• T4 (01:00:02.000): Bucket is refilled with all 5 tokens.
• T5 (01:00:02.100): 1 request arrives, consumes 1 token, 3 tokens left.
• T6 (01:00:03.000): No more requests so far. Bucket is refilled back to 4 tokens (adds 3 missing ones).

See more details information about the Token Bucket implementation in our docs here.

---

Leaking Bucket

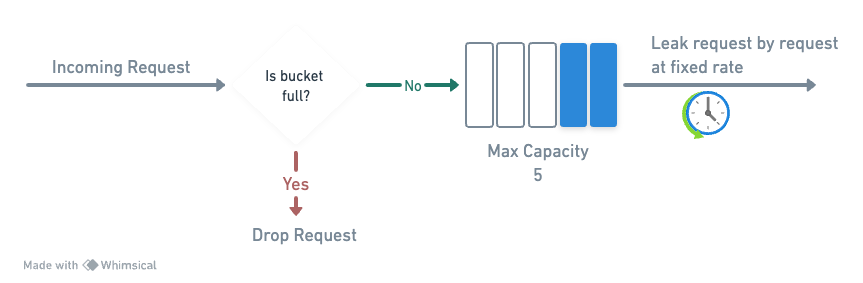
The leaking bucket algorithm is a rate limiting algorithm that is similar to the token bucket algorithm. The leaking bucket algorithm is based on the concept of a bucket that holds a fixed amount of water. The bucket has a maximum capacity, and the amount of water in the bucket is never greater than the capacity.

• The bucket has a leak rate, which determines the rate at which water leaks out of the bucket.
• When a request arrives, the algorithm checks if there is enough water in the bucket to serve the request.
• If there is enough water, the request is served, and the amount of water in the bucket is decremented.
• If there is not enough water, the request is rejected.
• Periodically, the bucket leaks water at a fixed rate.
• The rate at which the bucket leaks water determines the maximum rate at which requests can be served.
• The bucket has a maximum capacity, and the amount of water is never greater than the capacity.

Example: bucketSize = 4, leakRate = 1 request/2 sec.

• T0 (01:00:00): Bucket empty, 1 request arrives and enters the queue.
• T1 (01:00:02): 1st request processed (leaked out), 3 more arrive and queue up.
• T2 (01:00:03): Requests arrinving at this time are all dropped, because queue if full.
• T3 (01:00:04): 2nd request processed, 2 in queue, new requests continue to queue if space.

---

Fixed Window Counter

The fixed window counter algorithm is based on the concept of a fixed time window. The algorithm counts the number of requests that arrive within the time window and compares the count to a threshold. If the count exceeds the threshold, the request is rejected.

note

A major drawback of the fixed window counter algorithm is that it is susceptible to bursts of traffic at the edges of time windows, which can cause more requests than the allowed quota to go through. The excess can go as high as double the limit across two windows.

• The algorithm counts requests in fixed time windows.
• Excess requests are dropped once the limit is reached.
• The algorithm is susceptible to bursts at window boundaries, potentially allowing double the limit across two windows.
• The window size and the maximum number of requests are configurable.
• The algorithm is simple and efficient but has limitations in handling bursts of traffic.
• The algorithm is suitable for scenarios where a simple and efficient rate limiting mechanism is required and the limitations of the algorithm are acceptable.

Example: windowSize = 1 sec, requestLimit = 3.

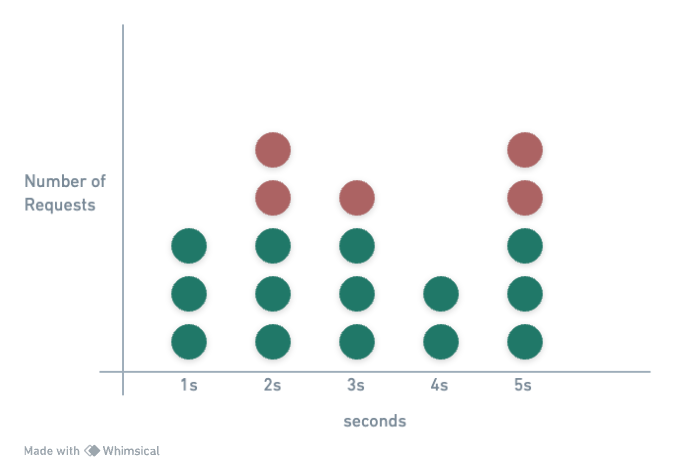
A problem with this algorithm is that a burst of traffic at the edges of time windows could cause more requests than allowed quota to go through. Consider the following case:

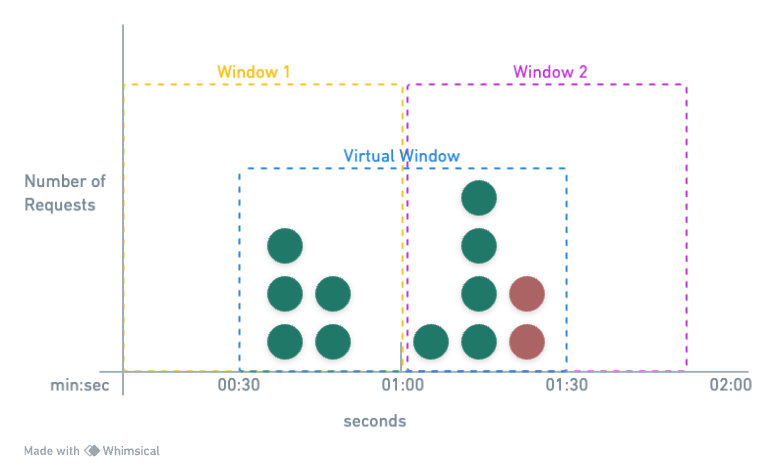
In Figure above, the system allows a maximum of 5 requests per minute, and the available quota resets at the human-friendly round minute. As seen, there are five requests between 00:00 and 01:00 and five more requests between 01:00 and 02:00. For the one-minute window between 00:30 and 01:30, 10 requests go through. That is twice as many as allowed requests.

---

Sliding Window Log

The sliding window log algorithm is based on the concept of a sliding time window. The algorithm maintains a log of timestamps for each request and provides an exact count within the sliding window. The algorithm enables accurate rate limiting by considering the exact timing of requests.

• The algorithm maintains a log of timestamps for each request.
• The algorithm provides an exact count within the sliding window.
• The algorithm enables accurate rate limiting by considering the exact timing of requests.
• The window size and the maximum number of requests are configurable.
• The algorithm is suitable for scenarios where maintaining an accurate request count is crucial.
• The algorithm has a higher memory overhead due to the need to maintain a log of timestamps for each request.

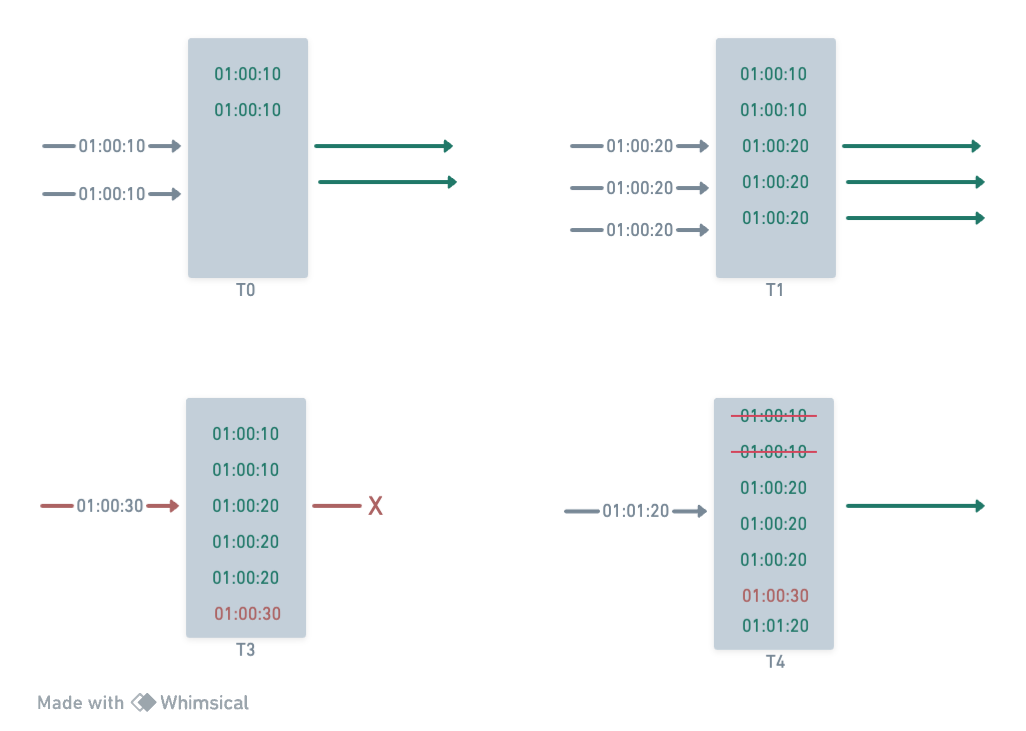
Example: windowSize = 1 min, maxRequests = 5.

• T0 (01:00:00): Window starts, request log is empty.
• T1 (01:00:10): 2 requests arrive, timestamps [01:00:10, 01:00:10] logged.
• T2 (01:00:20): 3 requests arrive, timestamps [01:00:20, 01:00:20, 01:00:20] logged.
• T3 (01:00:30): 1 request arrives, timestamp [01:00:30] logged. But the window is full, so the request is dropped.
• T4 (01:01:20): Now the logs before 01:00:20 are cleared, and the new request is allowed. Because the window is sliding, and the window has room for more requests.

---

Sliding Window Counter with Slots

The sliding window counter with slots algorithm is a variation of the sliding window counter algorithm. The algorithm divides the window into smaller slots for a more granular count and slides the window by updating slot counts, allowing a smooth transition and more evenly distributed rate limiting. The algorithm approximates actual sliding window behavior with improved performance.

• The algorithm divides the window into smaller slots for a more granular count.
• The algorithm slides the window by updating slot counts, allowing a smooth transition and more evenly distributed rate limiting.
• The algorithm approximates actual sliding window behavior with improved performance.
• The window size and the maximum number of requests are configurable.
• The algorithm is suitable for scenarios where a more evenly distributed rate limiting mechanism is required.
• The algorithm has a lower memory overhead due to the use of slots for a more granular count.

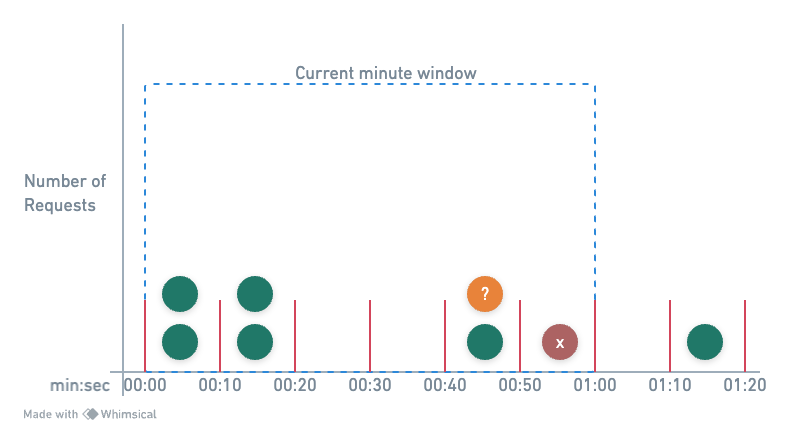
Example: windowSize = 1 min, slots = 6 (10 sec/slot), maxRequests = 10.

• T0 (01:00:00): Window starts, 6 slots initialized with 0 requests.
• T1 (01:00:20): 4 requests arrive, distributed in the first 2 slots.
• T2 (01:00:40): Window slides, first 2 slots cleared, 4 requests in next 2 slots.
• T3 (01:00:50): 3 more requests, fit into the 5th slot, total 7 requests allowed.

---

Approximate Sliding Window Counter

The approximate sliding window counter algorithm is a simple and efficient way to control the rate of requests to a resource. It is widely used in network traffic shaping, API rate limiting, and other scenarios where a controlled flow of requests is required.

The approximate sliding window counter algorithm is based on the concept of a sliding time window. The algorithm maintains a count of requests within the sliding window and provides an approximate count within the window.

The algorithm utilizes current and previous window counts with a weighting system based on time elapsed in the current window. The algorithm offers a balance between accuracy and efficiency, smoothing out traffic spikes with minimal memory usage.

• The formula for the weighted count is currentCount + previousCount * (1 - timeElapsed/windowSize).
• The algorithm utilizes current and previous window counts with a weighting system based on time elapsed in the current window.
• The algorithm offers a balance between accuracy and efficiency, smoothing out traffic spikes with minimal memory usage.
• The window size and the maximum number of requests are configurable.
• The algorithm is suitable for use cases where an exact count is less critical.
• The algorithm has a lower memory overhead due to the use of a weighted count.

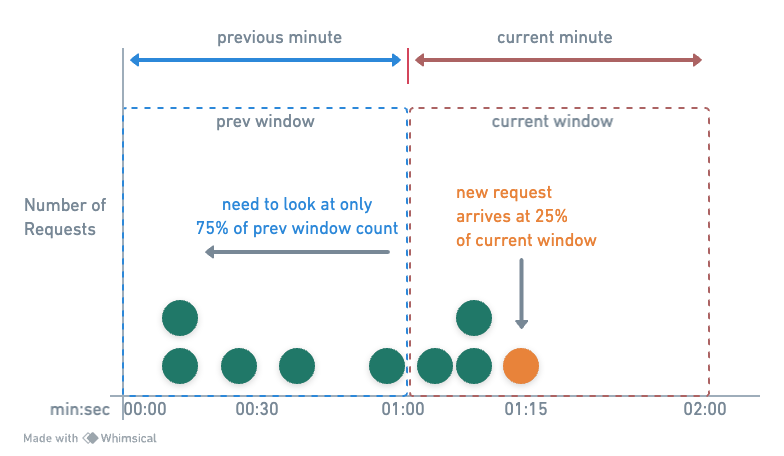
Example: windowSize = 1 min, requestLimit = 7

• T0 (01:00:00): Window starts, 0 requests counted.
• T1 (01:01:10): Previous window had 5 requests, current window has 2.
• T2 (01:01:15): New request evaluated with weighted count: 2 (current) + 5 * 0.75 (previous weighted) = 5.75, rounded down to 5, request allowed.
• T3 (01:02:00): Window resets, counting starts afresh for the new minute.

---

How to use it with minimalist-java

Use the RateLimitFactory to get a default instance of a rate limiter implementation or to customize the init config.

public class Main {

    public static void main(String[] args) {
        Api.create(8080).rateLimit(
                RateLimitFactory.customFixedWindowCounter(3, Duration.ofSeconds(1)))
            .addRoute(Route.builder("/").path(RouteMethod.GET, "/",
                ctx -> ResponseEntity.ok(Map.of("message", "Hello World!"))
            )).start();
    }

}

References

• https://systemsdesign.cloud/SystemDesign/RateLimiter